 O desafio é simples e, talvez, muitos já tenham se deparado com ele antes(ou não). Encontre uma maneira de dispor as 8 rainhas no tabuleiro de forma que nenhuma fique sob "ataque" de outra.
O desafio é simples e, talvez, muitos já tenham se deparado com ele antes(ou não). Encontre uma maneira de dispor as 8 rainhas no tabuleiro de forma que nenhuma fique sob "ataque" de outra.Observações:
1ª: A graça desse tipo de jogo é o SEU raciocínio para encontrar a solução. Portanto, pesquisar no Google(ou em outro motor de busca), só em caso de desistência.
______________________________________________________________________________
O problema das oito damas é o problema matemático de dispor oito damas em um tabuleiro de xadrez de dimensão 8x8, de forma que nenhuma delas seja atacada por outra. Para tanto, é necessário que duas damas quaisquer não estejam numa mesma linha, coluna, ou diagonal. Este é um caso específico do Problema das n damas, no qual temos n damas e um tabuleiro com n×n casas(para qualquer n ≥ 4).
História
O problema foi inicialmente proposto na revista Schachzeitung pelo enxadrista Max Bezzel em 1848, e ao longo dos anos foi avaliado por diversos matemáticos incluindo Gauss e Georg Cantor. A primeira solução foi proposta em 1850 por Franz Nauck, que também o generalizou para o Problema das n damas.
Soluções
O problema possui 92 soluções distintas, que podem ser obtidas a partir de um conjunto de 12 soluções únicas, aplicando operações de simetria (rotação e reflexão).
Construindo uma solução
Encontrar uma solução para este problema não é assim tão fácil. Utilizando análise combinatória podemos perceber que existem- 8! = 40320
Pode-se assim diminuir o tempo em que um algoritmo que solucione o problema é executado.
________________________
Fonte e respostas do desafio: AQUI!
________________________
Eu tentei durante 5 minutos e desisti.
E aí, alguém conseguiu?
Comente.

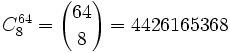
![P\left[A\right]=92/4426165368](http://upload.wikimedia.org/wikipedia/pt/math/e/e/4/ee43dd0086ea8d97dbc21c3b99fb4430.png)
![P\left[A\right]=92/40320](http://upload.wikimedia.org/wikipedia/pt/math/4/0/0/400d10fc58a0470cdef90dd1735f5968.png)
Um comentário:
Eu achei o desafio muito simples e fácil, sinceramente, muito fácil, resolvi em questão de 1 minuto, ao colocar as 4 primeiras damas achei que ficaria difícil colocar as restantes, que nada, consegui do mesmo modo, e não é só isso, existem varias posições que você pode deixar as peças para a resolução do problema. Não é tão complicado quanto parece, é simples. A propósito, não estou mentindo caso duvidem de mim, não estou me gabando, mas digamos que sou bem inteligente, tenho 163 de QI e passei no ITA-SP. Além de ser exímio enxadrista.
Postar um comentário